Procesamiento Digital de Imágenes (PDI)

Las transformaciones más simples, son las de los niveles de gris. Estos valores están relacionados por la expresión s=T(r), donde T es la transformación que mapea los valores de los pixeles r a los valores de los pixeles s. Estos valores se almacenan en un arreglo de 8 bits que tendrá 256 niveles.

Operaciones Puntuales

Las operaciones puntuales toman un pixel y lo modifican mediante una función de transformación.

Negativo de una imagen

Se obtiene utilizando a la función de transformación s =T(r). Para el rango [0, L-1] .

Se calcula con la siguiente fórmula: g(x, y) = (L-1)-f(x, y)

¿Cuándo se aplica este proceso? Es conveniente cuando queremos realzar detalles blancos o grises sobre un fondo oscuro. El contenido de información es el mismo.

He aquí el código en Python:

# l es igual al número de niveles de gris l= 256
def negative(l):
    #Cargar imagen
    img = cv2.imread("image/Milla.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros((rows, columns), dtype = np.uint8)
    for x in range(rows):
        for y in range(columns):
            img2[x, y] = (l-1)-img[x,y]
    cv2.imshow('Original',img)
    cv2.imshow('Negative',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()
    return

Resultados:

Aumento de la intensidad

La intensidad de cada píxel corresponde al brillo promedio o "radiancia" medida electrónicamente sobre el área del terreno que corresponde a cada píxel. Normalmente un píxel contiene información en un rango de 128 o 256 valores de gris por lo que se puede tener así una imagen monocroma.

Se calcula mediante la siguiente fórmula: g(x, y) = m*f(x, y)+b

Algoritmo:
1.- f= leemos imagen oscura
2.- Calculamos el tamaño de f
3.- Crear una matriz
4.- ∑filas∑columnas
5.- g(x, y) = m*f(x, y)+b
6.- Mostrar original(f)
7.- Mostrar g
8.- Fin

Por convención, las medidas más intensas están codificadas en blanco y las más débiles en negro.

¿Cuando aplicar este proceso? Se aplica a imágenes muy oscuras.

He aquí el código en Python:

def intensidad():
    #Cargar imagen
    img = cv2.imread("image/paraguas.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros((rows, columns), dtype = np.uint8)
    m = 0.8
    b = 100
    for x in range(0,rows):
        for y in range(0,columns):
            img2[x,y]= m * img[x, y] + b
    
    cv2.imshow('Original',img)
    cv2.imshow('Intensidad',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()
    return

Resultados:

Aumento de contraste

Se entiende por CONTRASTE a la diferencia de tonos que hay entre las distintas zonas de la imagen. Una imagen resulta visible gracias a su diferencia de contraste respecto a los valores de los tonos que la rodean.

He aquí el código en Python:

def contraste():
    #Cargar imagen
    img = cv2.imread("image/oscura.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    minimo = np.min(img)
    print minimo
    maximo = np.max(img)
    print maximo
    img2 = np.zeros( (rows, columns), dtype = np.uint8)   
    for x in range(0,rows):
        for y in range(0,columns):
            img2[x, y] = (img[x,y]-minimo) * 255 / (maximo-minimo)
        print "*"
            
    cv2.imshow('original',img)
    cv2.imshow('Contraste',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Resultados:

Funciones de Transformación No-Lineal (Monotónicas)

Tranformaciones Logarítmicas

La forma general de una transformación Logarítmica es: s = Clog(1+r)

Donde C es una constante, y se asume que r >= 0.

La curva generada por esta transformación muestra como mapea un rango dinámico más angosto de niveles de gris bajos de la imagen de entrada a un rango más ancho de niveles en la imagen de salida. Lo opuesto también se cumple para valores altos en la imagen de entrada.

La función logarítmica tiene la importante característica que comprime el rango dinámico de imágenes con una variación muy grande de niveles de gris.

Algoritmo:

1.- f = leer imagen

2.- Calcular el tamaño de f

3.- Crear una matriz(tamaño, uint8)

4.- c=(255/log(1+f(x, y)))

5.-r = obtener el nivel máximo de gris de la matriz de entrada(f)

6.- ∑filas∑columnas

g = Clog(1+r)

7.- Mostrar f

8.- Mostrar g

9.- Fin

He aquí el código en Python:

def transformacionLogaritmica():
    #Cargar imagen
    img = cv2.imread("image/imagen3.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros( (rows, columns), dtype = np.uint8)
    r = np.max(img)
    print r
    c = 255/math.log10(1+r) 
    for x in range(0,rows):
        for y in range(0,columns):
            img2[x, y] = c*math.log10(1+img[x,y])
        
            
    cv2.imshow('Original',img)
    cv2.imshow('Logaritmica',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Resultados:

Transformación Exponencial

La forma general de una transformación exponencial es:

s = c r^γ

Las curvas de transformación exponencial para valores fraccionales de γ mapean un rango estrecho de entradas oscuras a un rango más amplio de valores de salida.

A diferencia de la función logarítmica, en la función exponencial tenemos una familia de curvas de transformación simplemente variando el valor de γ. Las curvas con valores γ > 1 tienen el efecto exactamente opuesto a las curvas con γ < 1.

Una gran variedad de dispositivos de adquisición, impresión y desplegado de imágenes responde de acuerdo a leyes de potencia. Como convención se utiliza como exponente a γ, y las transformaciones se conocen como corrección gama.

¿A qué tipo de imágenes se aplica esta función de transformación? Se aplica a imágenes oscuras con muy poco contraste.
La principal característica de este método es la manipulación del contraste de la imagen.

He aquí el código en Python:

def transformacionExponencial():
    #Cargar imagen
    img = cv2.imread("image/imagen7.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros( (rows, columns), dtype = np.uint8)
    
    gamma = 0.08
    c = 255/255**gamma
    
    for x in range(0,rows):
        for y in range(0,columns):
            img2[x, y] = c*img[x, y]**gamma        

    cv2.imshow('Original',img)
    cv2.imshow('Exponencial',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Resultados:

Transformaciones básicas del nivel de gris

Transformación Lineal Por Partes

La principal ventaja de esta función sobre la anteriormente discutida es que puede ser una función con una complejidad arbitraria.

¿En que caso podemos usar esta función de transformación?

Las imágenes de bajo contraste pueden ser resultado de una iluminación pobre, de un rango dinámico muy pequeño en el sensor de la imagen, o tal vez de parámetros de calibración erróneos en la apertura de los lentes durante la adquisición de la imagen.

La idea de la expansión del contraste es el de incrementar el rango dinámico de los niveles de gris de la imagen de entrada.

Utilizaremos la siguiente fórmula para realizar este proceso:

Donde:
r, s ε[0:L-1]
α, β, γ ganancias de cada tramo
a, b, L-1 intervalos de ganancia

He aquí el código en Python:
Los casos especiales sirven para resaltar un rango específico de niveles de gris en una imagen. Las aplicaciones incluyen resaltar características como masas de agua en imágenes de satélite, resaltar defectos en imágenes de Rayos-X, etc.

Primer Caso Especial

Binarización

Este proceso desplega un valor alto de nivel de gris para todos los niveles de gris en el rango de interés y establecer valores bajos para todos los demás niveles produciendo una imagen binaria.

Las imágenes binarias siempre se obtienen a partir de imágenes de niveles de gris. En la actualidad no existen cámaras comerciales que proporcionen imágenes binarias. El proceso de conversión de una imagen de nivel de gris a una imagen formada sólo por dos valores o etiquetas(0 para el negro y 1 para el blanco) se conoce como binarización.

La binarización tiene una gran utilidad en procesamiento automático de imagen pues reduce enormemente la cantidad de datos de la imagen de una forma muy sencilla.

¿En qué casos utilizar este método? se emplea para separar las regiones u objetos de interés en una imagen del resto. Las imágenes binarias se usan en operaciones booleanas o lógicas para identificar individualmente objetos de interés o para crear máscaras sobre regiones.

He aquí el código en Python:

def primerCasoEspecial():
    #Cargar imagen
    img = cv2.imread("image/imagen3.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros( (rows, columns), dtype = np.uint8)
    
    #intervalos
    a = 50
    b = 100

    for x in range(0,rows):
        for y in range(0,columns):
            r = img[x][y]
            if a <=r and r<=b:
                img2[x][y] = 255
            else:
                img2[x][y] = 0
    cv2.imshow('Original',img)
    cv2.imshow('Transformacion Primer Caso Especial',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Segundo Caso Especial
Fraccionamiento del gris
Este proceso resalta el rango deseado de niveles de gris pero, preserva el fondo y las tonalidades de los niveles de gris de la imagen.

He aquí el código en Python:

def segundoCasoEspecial():
    #Cargar imagen
    img = cv2.imread("image/imagen3.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros( (rows, columns), dtype = np.uint8)
    
    #intervalos
    a = 50
    b = 200

    for x in range(0,rows):
        for y in range(0,columns):
            r = img[x][y]
            if a <=r and r<=b:
                img2[x][y] = 255
            else:
                img2[x][y] = img[x][y]
    cv2.imshow('Original',img)
    cv2.imshow('Transformacion Segundo Caso Especial',img2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Tercer Caso Especial

Threshold(Binarización por umbral)

¿Para qué utilizar este método? podemos utilizarlo para separar objetos de interés del resto de la imagen.

Procesamiento del Histograma

Histograma

El histograma de una imagen digital con niveles de gris en el rango [0, L-1] es una función discreta

h(r_k) = n_k, donde r_k is el k-ésimo nivel de gris y n_k es el número de píxeles en la imagen teniendo el nivel de gris r_k. Una práctica común para normalizar un histograma es dividiendo por los valores, por el número total de pixeles en la imagen, denotado por n. Así, un histograma normalizado es dado por p(r_k) = n_k/n, para k = 0,1...,L-1. hablando vagamente, p(r_k) da una estimación de la probabilidad de ocurrencia del nivel de gris r_k.

Nota que la suma de todos los componentes del histograma normalizado es igual a 1.
He aquí el código en Python:

def histograma():
    #Cargar imagen
    img = cv2.imread("image/imagen1.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    nivelesDeGris = numpy.zeros(256)    
    for x in range(0,rows):
        for y in range(0,columns):
            pixel = img[x][y]
            for ng in range(0,256):
                if pixel == ng:
                    nivelesDeGris[ng]= nivelesDeGris[ng]+1
    print nivelesDeGris
    plt.plot(nivelesDeGris,color="blue", linewidth=1.5, linestyle="-")
    plt.xlabel("Niveles de Gris")
    plt.ylabel("Numero de ocurrencias")
    plt.title("Histograma")
    plt.show()
    cv2.waitKey(0)
    cv2.destroyAllWindows()    
    return

Resultados:

Ecualización del Histograma

Mejora el contraste de la imagen. Reparte de forma más o menos los valores del histograma.
Dada una imagen MxM, con nsubk píxeles para cada rsubk, la ecualización de la histograma consiste en realizar la siguiente transformación sobre los niveles de intensidad de la imagen:
He aquí el código en Python:

def ecualizacionDelHistograma():
    #Cargar imagen
    img = cv2.imread("image/imagen5.jpg", cv2.IMREAD_GRAYSCALE)
    rows, columns = img.shape
    img2 = np.zeros( (rows, columns), dtype = np.uint8)
    
    nivelesDeGris = numpy.zeros(256, int)
    probabilidades = numpy.zeros(256, float)
    acum = numpy.zeros(256, float)
    eq = numpy.zeros(256, float)
    
    for x in range(0,rows):
        for y in range(0,columns):
            pixel = img[x][y]
            nivelesDeGris[pixel] = nivelesDeGris[pixel]+1
            
    totalPixeles = rows*columns
    
    for i in range(0, 256):
            probabilidades[i] = (probabilidades[i] + nivelesDeGris[i])/totalPixeles
    v=0
    for n in range(0, 256):
        v = v + probabilidades[n]
        acum[n] = v
       
    for k in range(0, 256):
        aux = round((acum[k] * 255)-1)
        if aux <= 0:
            aux = 0
            eq[k] = aux
        else:
            eq[k] = aux    
    
    l = 256
    sum = 0
            
    for x in range(0,rows):
        for y in range(0,columns):
            pixel = img[x][y]
            for ng in range(0, 256):
                if pixel == ng:
                    img2[x,y]= eq[ng]   
    plt.plot(nivelesDeGris,color="blue", linewidth=1.5, linestyle="-")
    plt.plot(eq,color="blue", linewidth=1.5, linestyle="-")
    plt.xlabel("Niveles de Gris")
    plt.ylabel("Numero de ocurrencias")
    plt.title("Histograma Ecualizado")
    cv2.imshow('Original',img)
    cv2.imshow('Transformacion del histograma',img2)
    plt.show()
    cv2.waitKey(0)
    cv2.destroyAllWindows()
    return

Brillo

Es dado por el valor medio de los niveles de gris.

Varianza

Indica la dispersión de los niveles de grises en una imagen.

Asimetría

Tiene como referencia la media en la distribución de los niveles de gris.

Energía

Es el grado de dispersión de los niveles de gris en la imagen.

Entropía

También informa sobre la distribución de los niveles de gris en la imagen.

Filtrado

Filtrar una imagen(f) consiste en aplicar una función de transformación(T) para tener una nueva imagen(g) de forma tal que ciertas características sean acentuadas o disminuidas.

La idea de hacer un filtrado de la imagen es reforzar o suavizar los contrastes espaciales existentes entre los valores de los pixeles, transformando esos valores para que se asemejen o se diferencien más a los pixeles vecinos.

Referencias

González, R.C., Wintz, P. (1996), Procesamiento digital de imágenes. AddisonWesley, Tema 3,4, pág 89-269.

http://arantxa.ii.uam.es/~eloy/html/doctorado/doct_9.pdf

Apellido, A. (14 de noviembre de 2016). Procesamiento Digital de imágenes [Mensaje en un blog]. Recuperado de http://pdi-biologia-unam.blogspot.mx/

http://alojamientos.us.es/gtocoma/pid/tema1-2.pdf

http://turing.iimas.unam.mx/~elena/PDI-Mast/Tema_6_D.pdf

http://turing.iimas.unam.mx/~elena/PDI-Mast/Tema_3_AB.pdf

http://www.librovision.eii.uva.es/pdf/cap4.pdf

http://www.dimages.es/Tutorial%20A.I/segmentacion/binaria.htm

Buscar este blog

Procesamiento Digital de Imágenes (PDI)

Operaciones Puntuales

Negativo de una imagen

Aumento de la intensidad

Aumento de contraste

Funciones de Transformación No-Lineal (Monotónicas)

Tranformaciones Logarítmicas

Transformación Exponencial

Transformaciones básicas del nivel de gris

Transformación Lineal Por Partes

Primer Caso Especial

Binarización

Procesamiento del Histograma

Histograma

Resultados:

Ecualización del Histograma

Brillo

Varianza

Asimetría

Energía

Entropía

Filtrado

Referencias

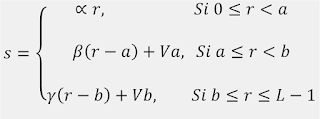
Comentarios

Publicar un comentario